So we are on the cusp of being able to dump more vintage Tama ROMs, since more are starting to be imaged.

This has already been done once, since the English P1 ROM is floating around and can be run in MAME.

So my question is, HOW???? was this process done. It has not really been documented.

In this page I'm going to document my attempt to recreate the P1 ROM from the image. This will serve as a template for the process on other vintage Tamas.

Basic notes about the P1 ROM, comparisons against the datasheet

• The size of the P1 ROM file (tama.b) is 12288 bytes.
• The size of an instruction in the P1 CPU architecture is 12 bits. Note that there is no data in the P1 CPU, everything is an instruction.
• We can see this in the structure of the ROM when we hexdump -C the file, and confirm it on Ghidra:
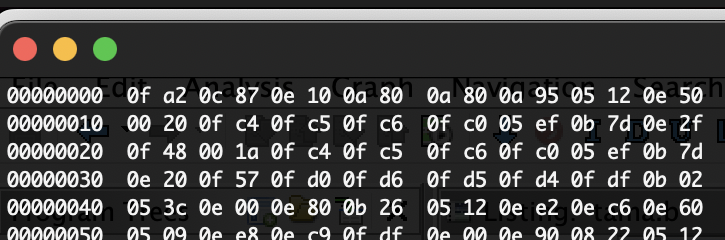
  So the first instruction is 0x0fa2, the next one is 0x0c87, etc. Note that an extra 4 bits of zeros are prepended to each instruction, so that each instruction in the ROM is exactly 2 bytes. We will need to mimic this structure when outputting the final ROM.
• The extra 4 bits of zeros were artificially added to the ROM file and are not going to be present on the ROM image itself. So 25% of the file is just padding. This means that the actual number of bits in the ROM, that we expect to see in the ROM image, is 12288 * 8 * 3 / 4 = 73728 bits.
• Here is a bird's eye view of the ROM:
  We need to figure out how to read the bits off this. But first it might be nice to get an idea of the high-level structure.
• Notice how there are 3 large rectangles, and each one is subdivided into what appear to be 48 smaller rectangles. (at first glance it looks like 96 but dealing with them in this larger unit will make more sense in a second)
• Knowing there are 73728 bits in the ROM, we expect that each rectangle should have 73728 / (48 * 3) = 512 bits.
• Unfortunately there's a lot that we don't know yet, like we don't know how each bit we find on the ROM image maps to a bit in the ROM file. That'll just be part of the learning process... (I think the tools we'll be working with can solve for this too)
• A single rectangle is shown here, zoomed in:
• The leftmost and rightmost columns appear to be a repeating pattern. So ignoring those, we see that each horizontal row has 16 bits in it, and there are 32 rows. So this gives us 512 bits in the rectangle, which aligns exactly with the number I expected. This means I have a good idea of how to identify the bits in the picture.
• It's kind of interesting to me at this point that I don't see anything being done in obvious units of 12 that would indicate an instruction. Oh well

maskroomtool